Again Considering at the Point Where C Passes Through the Origin
3. Derivatives
3.2 The Derivative as a Function
Learning Objectives
- Ascertain the derivative function of a given function.
- Graph a derivative function from the graph of a given office.
- Land the connection between derivatives and continuity.
- Depict three weather for when a function does non have a derivative.
- Explain the meaning of a college-order derivative.
Equally we accept seen, the derivative of a part at a given point gives united states of america the rate of change or slope of the tangent line to the office at that point. If nosotros differentiate a position function at a given fourth dimension, we obtain the velocity at that time. It seems reasonable to conclude that knowing the derivative of the function at every bespeak would produce valuable information well-nigh the behavior of the function. Nonetheless, the process of finding the derivative at fifty-fifty a handful of values using the techniques of the preceding section would apace become quite tedious. In this department nosotros define the derivative function and learn a procedure for finding information technology.
Derivative Functions
The derivative function gives the derivative of a role at each point in the domain of the original function for which the derivative is divers. Nosotros tin formally define a derivative part as follows.
Definition
Permit ![]() be a function. The derivative function, denoted by
be a function. The derivative function, denoted by ![]() , is the function whose domain consists of those values of
, is the function whose domain consists of those values of ![]() such that the post-obit limit exists:
such that the post-obit limit exists:
![]() .
.
A function ![]() is said to be differentiable at
is said to be differentiable at ![]() if
if
![]() exists. More generally, a function is said to exist differentiable on
exists. More generally, a function is said to exist differentiable on ![]() if information technology is differentiable at every point in an open set
if information technology is differentiable at every point in an open set ![]() , and a differentiable office is one in which
, and a differentiable office is one in which ![]() exists on its domain.
exists on its domain.
In the next few examples we utilize (Effigy) to discover the derivative of a function.
Finding the Derivative of a Foursquare-Root Office
Find the derivative of ![]() .
.
Solution
Beginning directly with the definition of the derivative part. Use (Figure).
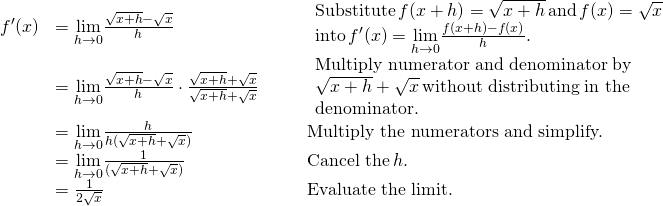
Finding the Derivative of a Quadratic Function
Find the derivative of the function ![]() .
.
Solution
Follow the same procedure here, simply without having to multiply by the conjugate.
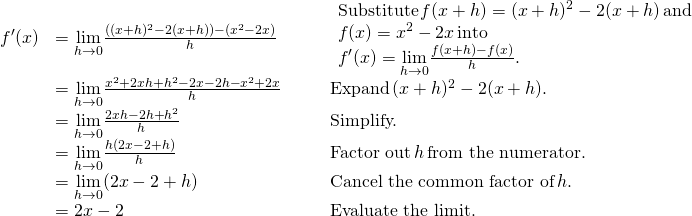
Find the derivative of ![]() .
.
Solution
![]()
Nosotros use a variety of different notations to limited the derivative of a function. In (Figure) we showed that if ![]() , then
, then ![]() . If we had expressed this part in the class
. If we had expressed this part in the class ![]() , nosotros could have expressed the derivative every bit
, nosotros could have expressed the derivative every bit ![]() or
or ![]() . Nosotros could take conveyed the same information by writing
. Nosotros could take conveyed the same information by writing ![]() . Thus, for the role
. Thus, for the role ![]() , each of the following notations represents the derivative of
, each of the following notations represents the derivative of ![]() :
:
![]() .
.
In place of ![]() nosotros may also apply
nosotros may also apply ![]() Use of the
Use of the ![]() annotation (called Leibniz notation) is quite mutual in applied science and physics. To sympathise this notation improve, call back that the derivative of a role at a betoken is the limit of the slopes of secant lines every bit the secant lines approach the tangent line. The slopes of these secant lines are often expressed in the course
annotation (called Leibniz notation) is quite mutual in applied science and physics. To sympathise this notation improve, call back that the derivative of a role at a betoken is the limit of the slopes of secant lines every bit the secant lines approach the tangent line. The slopes of these secant lines are often expressed in the course ![]() where
where ![]() is the deviation in the
is the deviation in the ![]() values corresponding to the departure in the
values corresponding to the departure in the ![]() values, which are expressed equally
values, which are expressed equally ![]() ((Figure)). Thus the derivative, which tin can be thought of as the instantaneous charge per unit of change of
((Figure)). Thus the derivative, which tin can be thought of as the instantaneous charge per unit of change of ![]() with respect to
with respect to ![]() , is expressed as
, is expressed as
![]() .
.
Graphing a Derivative
Nosotros accept already discussed how to graph a function, so given the equation of a function or the equation of a derivative part, we could graph it. Given both, nosotros would expect to come across a correspondence between the graphs of these 2 functions, since ![]() gives the rate of change of a role
gives the rate of change of a role ![]() (or slope of the tangent line to
(or slope of the tangent line to ![]() ).
).
In (Effigy) we found that for ![]() . If we graph these functions on the same axes, equally in (Figure), we can utilise the graphs to understand the relationship between these two functions. Kickoff, we notice that
. If we graph these functions on the same axes, equally in (Figure), we can utilise the graphs to understand the relationship between these two functions. Kickoff, we notice that ![]() is increasing over its entire domain, which ways that the slopes of its tangent lines at all points are positive. Consequently, we look
is increasing over its entire domain, which ways that the slopes of its tangent lines at all points are positive. Consequently, we look ![]() for all values of
for all values of ![]() in its domain. Furthermore, as
in its domain. Furthermore, as ![]() increases, the slopes of the tangent lines to
increases, the slopes of the tangent lines to ![]() are decreasing and we expect to see a corresponding decrease in
are decreasing and we expect to see a corresponding decrease in ![]() . We besides discover that
. We besides discover that ![]() is undefined and that
is undefined and that ![]() , corresponding to a vertical tangent to
, corresponding to a vertical tangent to ![]() at 0.
at 0.
In (Figure) we plant that for ![]() . The graphs of these functions are shown in (Effigy). Discover that
. The graphs of these functions are shown in (Effigy). Discover that ![]() is decreasing for
is decreasing for ![]() . For these same values of
. For these same values of ![]() . For values of
. For values of ![]() is increasing and
is increasing and ![]() . Also,
. Also, ![]() has a horizontal tangent at
has a horizontal tangent at ![]() and
and ![]() .
.
Sketching a Derivative Using a Function
Use the following graph of ![]() to sketch a graph of
to sketch a graph of ![]() .
.
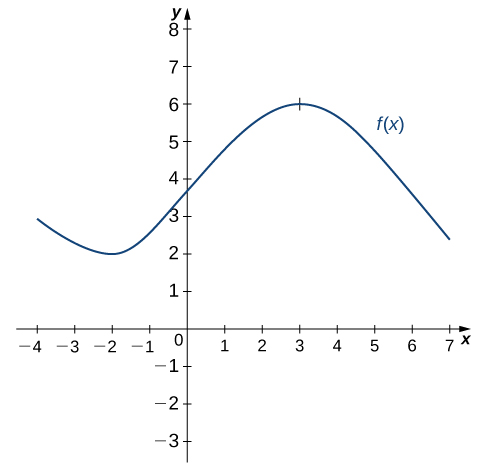
Sketch the graph of ![]() . On what interval is the graph of
. On what interval is the graph of ![]() higher up the
higher up the ![]() -centrality?
-centrality?
Solution
![]()
Derivatives and Continuity
Now that we tin can graph a derivative, let's examine the behavior of the graphs. Outset, we consider the relationship between differentiability and continuity. We will see that if a part is differentiable at a point, information technology must be continuous there; however, a role that is continuous at a point need not be differentiable at that indicate. In fact, a function may be continuous at a indicate and fail to be differentiable at the signal for one of several reasons.
Proof
If ![]() is differentiable at
is differentiable at ![]() , then
, then ![]() exists and
exists and
![]() .
.
We want to bear witness that ![]() is continuous at
is continuous at ![]() by showing that
by showing that ![]() . Thus,
. Thus,
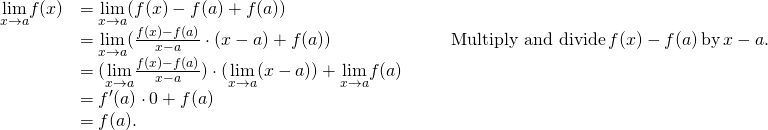
Therefore, since ![]() is defined and
is defined and ![]() , we conclude that
, we conclude that ![]() is continuous at
is continuous at ![]() .
. ![]()
We take just proven that differentiability implies continuity, only now we consider whether continuity implies differentiability. To determine an answer to this question, we examine the part ![]() . This function is continuous everywhere; however,
. This function is continuous everywhere; however, ![]() is undefined. This ascertainment leads usa to believe that continuity does not imply differentiability. Let'due south explore further. For
is undefined. This ascertainment leads usa to believe that continuity does not imply differentiability. Let'due south explore further. For ![]() ,
,
![]() .
.
This limit does not exist considering
![]() .
.
See (Figure).
Let'due south consider some additional situations in which a continuous role fails to be differentiable. Consider the function ![]() :
:
![]() .
.
Thus ![]() does not exist. A quick look at the graph of
does not exist. A quick look at the graph of ![]() clarifies the situation. The function has a vertical tangent line at 0 ((Figure)).
clarifies the situation. The function has a vertical tangent line at 0 ((Figure)).
The function 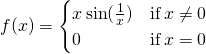 too has a derivative that exhibits interesting behavior at 0. Nosotros come across that
too has a derivative that exhibits interesting behavior at 0. Nosotros come across that
![]() .
.
This limit does non exist, essentially because the slopes of the secant lines continuously change direction every bit they approach zero ((Figure)).
In summary:
- We discover that if a function is not continuous, it cannot be differentiable, since every differentiable part must be continuous. However, if a function is continuous, it may still fail to be differentiable.
- Nosotros saw that
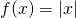 failed to exist differentiable at 0 because the limit of the slopes of the tangent lines on the left and right were not the aforementioned. Visually, this resulted in a sharp corner on the graph of the function at 0. From this we conclude that in order to be differentiable at a bespeak, a role must exist "smooth" at that point.
failed to exist differentiable at 0 because the limit of the slopes of the tangent lines on the left and right were not the aforementioned. Visually, this resulted in a sharp corner on the graph of the function at 0. From this we conclude that in order to be differentiable at a bespeak, a role must exist "smooth" at that point. - As we saw in the example of
![Rendered by QuickLaTeX.com f(x)=\sqrt[3]{x}](https://opentextbc.ca/calculusv1openstax/wp-content/ql-cache/quicklatex.com-c3c5e7be9bc257eb2866277bae5be644_l3.png) , a office fails to exist differentiable at a point where at that place is a vertical tangent line.
, a office fails to exist differentiable at a point where at that place is a vertical tangent line. - As we saw with
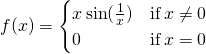 a part may fail to be differentiable at a betoken in more complicated means besides.
a part may fail to be differentiable at a betoken in more complicated means besides.
A Piecewise Part that is Continuous and Differentiable
Solution
For the part to be continuous at ![]() . Thus, since
. Thus, since
![]()
and ![]() , nosotros must accept
, nosotros must accept ![]() . Equivalently, nosotros take
. Equivalently, nosotros take ![]() .
.
For the function to exist differentiable at -10,
![]()
must be. Since ![]() is divers using different rules on the right and the left, we must evaluate this limit from the right and the left and then set up them equal to each other:
is divers using different rules on the right and the left, we must evaluate this limit from the right and the left and then set up them equal to each other:
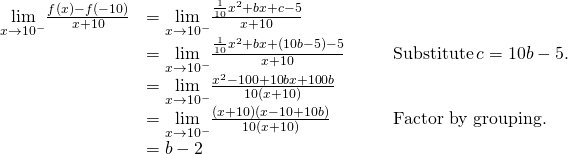
Nosotros also have
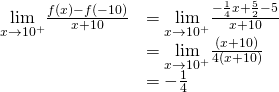
This gives usa ![]() . Thus
. Thus ![]() and
and ![]() .
.
Higher-Gild Derivatives
The derivative of a part is itself a function, and so nosotros can notice the derivative of a derivative. For example, the derivative of a position part is the rate of change of position, or velocity. The derivative of velocity is the charge per unit of change of velocity, which is acceleration. The new function obtained by differentiating the derivative is called the 2nd derivative. Furthermore, we tin continue to take derivatives to obtain the third derivative, fourth derivative, and so on. Collectively, these are referred to as higher-society derivatives. The annotation for the higher-lodge derivatives of ![]() can exist expressed in any of the following forms:
can exist expressed in any of the following forms:
![]()
![]()
![]() .
.
Information technology is interesting to annotation that the notation for ![]() may be viewed as an attempt to express
may be viewed as an attempt to express ![]() more compactly. Analogously,
more compactly. Analogously, ![]() .
.
Finding a Second Derivative
For ![]() , find
, find ![]() .
.
Solution
First find ![]() .
.
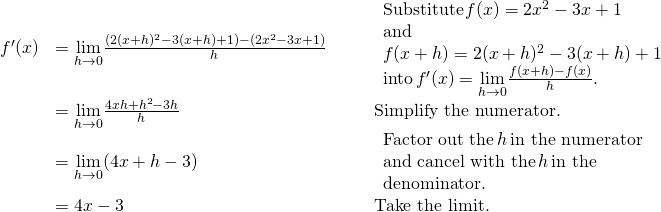
Adjacent, find ![]() by taking the derivative of
by taking the derivative of ![]() .
.
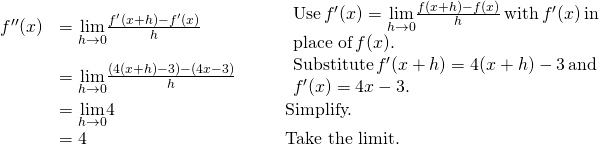
Finding Acceleration
The position of a particle forth a coordinate axis at fourth dimension ![]() (in seconds) is given past
(in seconds) is given past ![]() (in meters). Detect the function that describes its dispatch at fourth dimension
(in meters). Detect the function that describes its dispatch at fourth dimension ![]() .
.
Solution
Since ![]() and
and ![]() , nosotros begin by finding the derivative of
, nosotros begin by finding the derivative of ![]() :
:
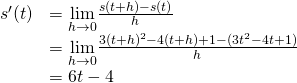
Side by side,
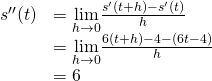
Thus, ![]() .
.
Key Concepts
Key Equations
- The derivative function
For the following exercises, apply the definition of a derivative to find ![]() .
.
i. ![]()
two. ![]()
3. ![]()
4. ![]()
Solution
![]()
five. ![]()
6. ![]()
Solution
![]()
seven. ![]()
8. ![]()
Solution
![]()
9. ![]()
10. ![]()
Solution
![]()
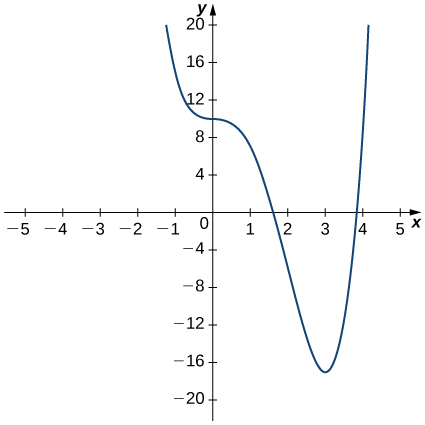
For the following exercises, use the graph of ![]() to sketch the graph of its derivative
to sketch the graph of its derivative ![]() .
.
xi. 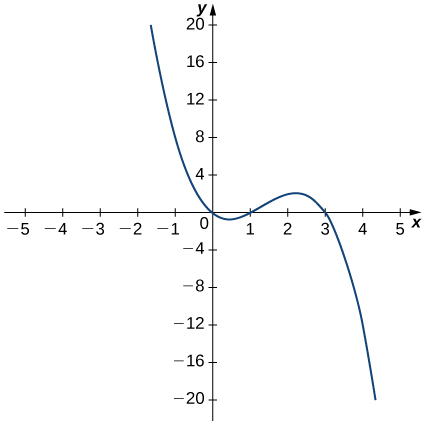
12. 
Solution

xiii. 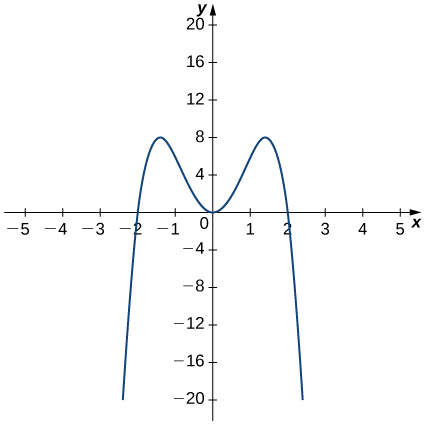
fourteen. 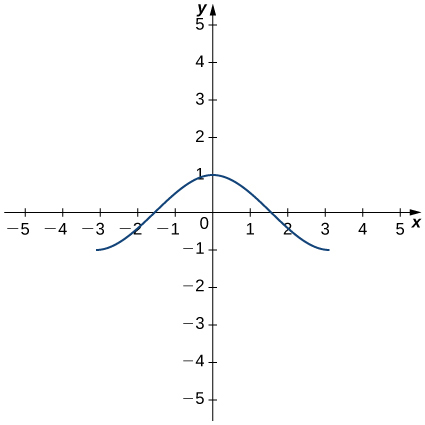
Solution

For the following exercises, the given limit represents the derivative of a function ![]() at
at ![]() . Find
. Find ![]() and
and ![]() .
.
15. ![]()
16. ![]()
Solution
![]()
17. ![]()
18. ![]()
Solution
![]()
19. ![]()
20. ![]()
Solution
![]()
For the post-obit functions,
- sketch the graph and
- utilize the definition of a derivative to testify that the part is not differentiable at
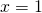 .
.
21. 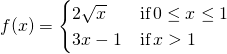
23. 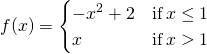
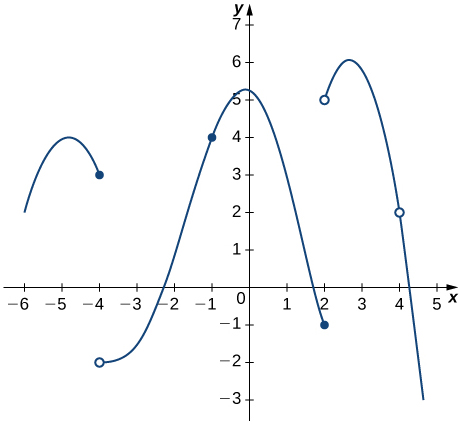
For the following graphs,
- determine for which values of
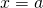 the
the 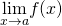 exists but
exists but 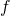 is non continuous at
is non continuous at 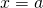 , and
, and - determine for which values of
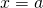 the office is continuous simply not differentiable at
the office is continuous simply not differentiable at 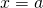 .
.
25. 
For the following functions, use ![]() to find
to find ![]() .
.
28. ![]()
29. ![]()
30. ![]()
Solution
![]()
For the post-obit exercises, use a calculator to graph ![]() . Decide the role
. Decide the role ![]() , then use a calculator to graph
, then use a calculator to graph ![]() .
.
31. [T] ![]()
33. [T] ![]()
35. [T] ![]()
For the following exercises, draw what the two expressions correspond in terms of each of the given situations. Be sure to include units.
37. ![]() denotes the population of a metropolis at time
denotes the population of a metropolis at time ![]() in years.
in years.
38. ![]() denotes the total amount of money (in thousands of dollars) spent on concessions by
denotes the total amount of money (in thousands of dollars) spent on concessions by ![]() customers at an amusement park.
customers at an amusement park.
Solution
a. Average rate at which customers spent on concessions in thousands per customer.
b. Rate (in thousands per client) at which ![]() customers spent coin on concessions in thousands per customer.
customers spent coin on concessions in thousands per customer.
39. ![]() denotes the total cost (in thousands of dollars) of manufacturing
denotes the total cost (in thousands of dollars) of manufacturing ![]() clock radios.
clock radios.
xl. ![]() denotes the class (in percentage points) received on a test, given
denotes the class (in percentage points) received on a test, given ![]() hours of studying.
hours of studying.
Solution
a. Average grade received on the exam with an average report time between two amounts.
b. Rate (in pct points per hr) at which the grade on the test increased or decreased for a given average study time of ![]() hours.
hours.
41. ![]() denotes the cost (in dollars) of a sociology textbook at academy bookstores in the United States in
denotes the cost (in dollars) of a sociology textbook at academy bookstores in the United States in ![]() years since 1990.
years since 1990.
42. ![]() denotes atmospheric pressure at an altitude of
denotes atmospheric pressure at an altitude of ![]() feet.
feet.
Solution
a. Boilerplate modify of atmospheric force per unit area between ii different altitudes.
b. Charge per unit (torr per foot) at which atmospheric pressure is increasing or decreasing at ![]() anxiety.
anxiety.
Solution
a. The rate (in degrees per foot) at which temperature is increasing or decreasing for a given acme ![]() .
.
b. The rate of change of temperature as altitude changes at m feet is -0.1 degrees per human foot.
Solution
a. The charge per unit at which the number of people who have come up down with the flu is irresolute ![]() weeks later the initial outbreak.
weeks later the initial outbreak.
b. The charge per unit is increasing sharply up to the third calendar week, at which betoken information technology slows downwardly and then becomes constant.
For the following exercises, use the post-obit table, which shows the height ![]() of the Saturn V rocket for the Apollo xi mission
of the Saturn V rocket for the Apollo xi mission ![]() seconds after launch.
seconds after launch.
| Time (seconds) | Height (meters) |
|---|---|
| 0 | 0 |
| one | ii |
| 2 | 4 |
| 3 | 13 |
| 4 | 25 |
| five | 32 |
47.What is the concrete meaning of ![]() ? What are the units?
? What are the units?
Source: https://opentextbc.ca/calculusv1openstax/chapter/the-derivative-as-a-function/
0 Response to "Again Considering at the Point Where C Passes Through the Origin"
Post a Comment